Components of the Decision-Support system

Components of the STS Decision-Support system

1. Planning Project Area

Gypsy moth populations do not spread continuously along the population front. Instead, isolated colonies become established beyond the population front mostly because of inadvertent transportation of life stages by humans. Thus, the area near the population front can be separated into the infested zone that is continuously occupied, transition zone where isolated colonies become established, and the uninfested zone where the probability of colony establishment is close to zero (Fig. 1). As isolated colonies grow, they coalesce and contribute to the expansion of the population front. The rate of spread can be reduced if isolated colonies in the transition zone are detected and suppressed or eradicated before they grow too large. Thus, the basic idea of the Slow the Spread project is to manage isolated populations in the transition zone in order to slow the progression of the population front.

Fig. 1. Spread of gypsy moth populations via establishment of isolated colonies beyond the advancing front.

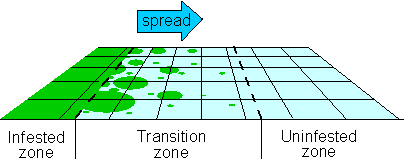
The following decision-support system for the STS project evolved during the initial pilot project. It is largely based on the optimization of a model of gypsy moth spread that quantifies possible effects of the STS project on the rate of population spread (Sharov et al. 1998b).

The project area is a barrier zone set along the expanding population front. Boundaries of the project are determined relative to population boundaries which are estimated from moth counts in grids of pheromone-baited traps (Sharov et al. 1995). Sharov et al. (1997) showed that the boundary determined using the 10 moths/trap threshold was most stable in space and time compared with population boundaries estimated using other thresholds from 1 to 300 moths/trap (see the analysis of variability of population boundaries). Thus, the location of the project area is adjusted relative to the 10 moths/trap line.

The project area is set on both sides from the 10 moths/trap line from the distance of at least 50 km before the line to at least 120 km beyond the line (Fig. 2). Isolated colonies of gypsy moth become established mostly up to 170 km from the 10 moth/trap line (Sharov and Liebhold 1997). However, the area beyond 120 km from the 10 moths/trap line is usually managed by eradication programs of the USDA APHIS.

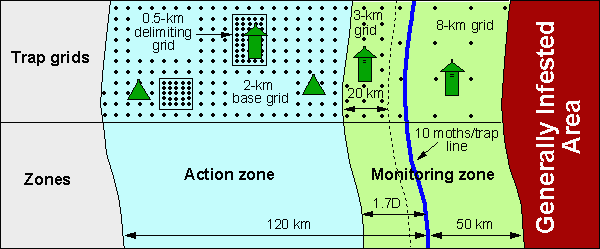
Fig. 2. Location of the STS project area, trap grids, and trap types used in various parts of the project; D is the distance between 10 and 30 moths/trap lines. If the 30 moths line is not available, then D equals the distance between 3 and 10 moth lines.

To avoid sharp turns in project boundaries, the 10 moths/trap line is smoothed using a 100-km averaging window. Because of smoothing, the project area will include bulges in the population front which are most threatening as footsteps for further population expansion (Fig. 3). In some areas (e.g., in the coastal plain of Virginia, and in Wisconsin), the 10 moth line changes considerably from year to year mostly due to the variation in long-distance male moth dispersal. To stabilize project boundaries, we use weighted averages of 10, and 30 moth lines in the current and past 2 years:

Z = (W₀X_t + W₁X_{t -1} + W₂X_{t -2}) / (W₀ + W₁ + W₂),

where Z is the averaged location of the 10 (or 30) moth line, X_t is the location of the moth line in the current year t, and W_i are weights that are equal to 0, 0.5, and 0.25 for i = 0, 1, and 2, respectively.

The project area is subdivided into the following two zones: (1) the monitoring zone is located in the portion of the area that faces the approaching population front, and (2) the action zone is located in the distant portion of the project area (Fig. 2).

The action zone is used for detecting and eradicating isolated colonies whereas the monitoring zone is used for delineating population boundaries, which are necessary for determining the location of the project area and for evaluating the effect of the project on the rate of population spread. In the Appalachian Mountains, the boundary between these two zones is located approximately 20 km beyond the 10 moths line (see historical maps of STS location). The background counts of male moths in pheromone traps in this area were generally low at distances beyond 20 km away from the 10 moths/trap line; thus isolated colonies were relatively easy to detect and delineate for treatment. However in other areas, male moth counts may be still high at 20 km beyond the 10 moths line. Thus, for the operational STS project we set the distance between the 10 moths line and the beginning of the action zone equal to the distance, D, between population boundaries estimated using thresholds of 10 and 30 moths/trap (or 10 and 3 moths/trap if the line of 30 moths/trap was not determined) multiplied by 1.7. The width of the action zone is a constant and is equal to 100 km.

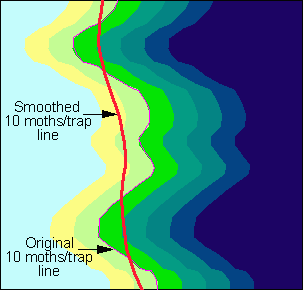
Fig. 3. Smoothing of the 10 moths/trap line. Shading represents moth counts in pheromone traps.

Principles of Monitoring

Gypsy moth populations are monitored using pheromone-baited traps. Traps are set before the start of the flight period and collected after flight termination. Dates of setting and collecting traps vary depending on the climate and can be predicted using our phenology model

In most of the monitoring zone, pheromone traps are set in grids with an intertrap distance of 8 km or 5 mi (Fig. 2). An intertrap distance of 8 km was shown to be sufficient for estimating population boundaries and for evaluating the effect of the STS project on the rate of spread (Sharov et al. 1997). In the area adjacent to the action zone, i.e., at distances <20 km (or 2 quads) from the action zone, the intertrap distance should be 3 km (2 mi). A higher trap density is needed in this area because the information about moth counts is used by the decision-algorithm model. All traps are milk carton traps.

The intertrap distance in the base grid of the action zone is 2 km, which was shown to be sufficient for detecting isolated colonies (Sharov et al. 1998b). In the areas that have a mile-based system of roads, we recommend setting trap grids diagonally, so that the intertrap distance would be 2.26 km. All traps are delta traps. The base grid is not set in the areas where delimiting grids or treatment evaluation grids are placed.

Delimiting grids are set in the areas that may contain isolated colonies of the gypsy moth. Areas are suggested for delimiting by the Decision Algorithm (DA) which is described in the next section. But the final decision to set a delimiting grid is made by people taking into account additional factors (financial, strategical, and political). The area for delimitation may be set a little larger or smaller than the area suggested by the DA in order to effectively detect the boundaries of the colony. Delimiting grids in the action zone are set with an intertrap distance of 0.5 km. In the area with a mile-based system of roads, delimiting grids should have a straight orientation and a 1/3 mi intertrap distance. If a colony is large (>1 quad) then a 1 km intertrap distance can be used in the delimiting grid.

All traps in delimiting grids are milk carton traps because moth counts may be large in the center of a colony. However, if the maximum moth count in the previous year was <= 5 moths, then delta traps may be used in the delimiting grid.

Post-treatment evaluation grids are set in the areas treated in the same year by pesticides, Bt, or virus; or in the areas where mating disruption was used in the previous year. The intertrap distance is 0.5 km (1/3 MI), and all traps are milk carton traps because catches may be still large if treatment was unsuccessful or partially successful. If the maximum moth count in the previous year was <= 50 moths, then delta traps may be used in the delimiting grid.

Decision algorithm

The Decision Algorithm (DA) is used to select areas in the action zone for delimiting grids and for treatment. This selection is done in two steps: (1) selection of potential problem areas, and (2) evaluation of potential problem areas.

Selection of potential problem areas

A potential problem area is an area where there is likely a reproducing population of the gypsy moth. We use three methods to detect potential problem areas and then overlay areas selected with each method.

Method 1: Finding traps that caught an unusually high number of male moths. A trap is selected if moth count exceed the 98th percentile of the local distribution of moth counts in the 40x40 km neighborhood. We assume that the probability distribution of loge(N+1) is normal (N = moth count in a trap). Percentile is determined from the local mean and S.D. of loge(N+1).
Method 2: Finding peaks in the interpolated surface of moth counts in pheromone traps. Interpolation is done using kriging (see appendix for details). Then we select those areas where interpolated values are above the 92nd percentile of the local distribution of interpolated values in the 40x40 km neighborhood. We assume that the probability distribution of loge(N+1) is normal (N = interpolated moth counts).
Method 3: Finding peaks in the product of interpolated surfaces of moth counts in the current and previous years. The idea behind this method is that by overlaying the data from two years we may be able to detect those potential problem area that are difficult to identify from one year's data (e.g., because of intensive male moth dispersal in a particular year). First, moth counts are interpolated using kriging in both years; then the product, Q, of log-transformed [loge(N+1)] interpolated values is estimated at each location. Finally, we select those areas where Q is above the 92nd percentile of the local distribution of Q values in the 40x40 km neighborhood.

Evaluation of potential problem areas

For each potential problem area (PPA) we collect the following information. By moth counts we mean counts in individual traps. Interpolated moth counts were not used here.
A = area of the PPA
d = distance from the beginning of the action zone (dist)
T = number of traps in the PPA
N(t) = maximum moth counts in the PPA
Na(t) = average log moth counts, loge(n+1), in the PPA in year t (t = current year)
Nb(t) = average log moth counts, loge(n+1), in the 25-km radius from the center of the PPA excluding traps located in this or other PPA ("b" stands for background moth abundance).
An = area of the PPA including a 3-km neighborhood of the PPA center ("n" stands for neighborhood). An example of area An is shown in Fig 4.
Tn = number of traps located in the area An.
N'(t-1) = maximum moth counts in the previous year in the An area for the current-year PPA.

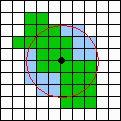
Fig. 4. Area An that consists of a PPA (green) plus a 3-km neighborhood of the PPA center (blue). The grid size is 1 km.

These characteristics are used to estimate the priority index, P, and delimiting index, D. The priority index indicates how important it is to manage the colony, and the delimiting index shows if the colony is sufficiently delimited for effective treatment. A colony is recommended for delimiting if
either TP₁ £ P £ TP₂,
or P ³ TP₁ and D £ TD,
where TP₁ and TP₁ are the first and second priority thresholds, and TD is the delimiting threshold (Fig. 5).

A colony is recommended for treatment if
P ³ TP₂ and D ³ TD,
where TP₂ is the second priority threshold, and TD is the delimiting threshold (Fig. 5).

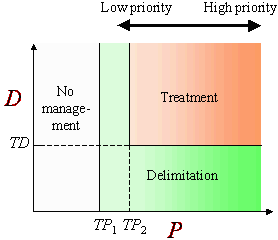
Fig. 5. STS decisions for a potential problem area with priority index, P, and delimiting index, D.

The priority index, P, is estimated with the equation:

P = F1(N(t), N'(t-1)) + F2(d) + F3(Nb(t)NB(t-1)) + F4

where F1 is a function of maximum moth counts in the PPA in the current and previous years; F2 is an adjustment to the distance from the beginning of the STS action zone; F3 is an adjustment to moth counts in the area around the PPA in the current and previous year, and F4 is an adjustment to the presence of other PPA located farther away from the population front.

Function F1 (Fig. 6) is given by the equation:

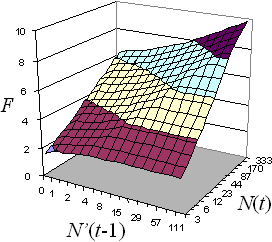
Fig. 6. The F1 component of the priority index is a function of maximum moth counts in the PPA in the current year, N(t), and previous year, N'(t-1).

We use N'(t-1) rather than N(t-1) because some PPA are as small as 1 sq. km., and may have only a few traps or no traps at all in the previous year.

Function F2 (Fig. 7) is given by the equation:

F2 = min(0.002d, 0.222d - 3.3)

where d is a distance from the PPA to the beginning of the STS action zone. F2 is negative for small distances, d, and slightly positive for large distances. This means that the priority of a PPA is decreased near the beginning of the STS action zone, and slightly increased for locations far away in the uninfested area.

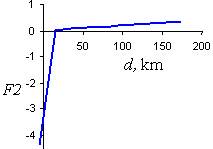
Fig. 7. The F2 component of the priority index is a function of distance, d from the PPA to the beginning of the STS action zone.

Function F3 is linear:

F3 = 0.5Nb(t-1) - 1.3Nb(t)

It decreases the priority of a PPA if the background moth abundance is high. Thus, priority of management is decreased in years characterized by intensive moth dispersal. On the contrary, background moth abundance in the previous year increases the priority of management. This means that if male moth dispersal has decreased in the current year causing a decrease in background moth abundance, then priorities of management are increased.

The last component, F4, of the priority index is estimated as a sum of "cones of influence" of other colonies:

where x_i is the distance from PPA evaluated to the i-th PPA measured in the direction perpendicular to the population front, and y_i is the distance between these PPAs in the direction parallel to the population front (see Fig. 8).

The sum in this equation is taken over all other PPAs that are (a) located farther away from the population front than the PPA being evaluated, (b) located within the STS action zone, and (c) have a priority index P > 2.5.

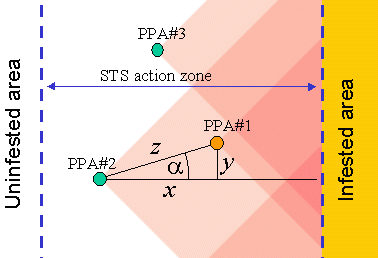
Fig. 8. Each PPA decreases the priority index of other PPAs located closer to the infested area within the cone of influence (pink). Dashed blue lines are boundaries of the STS action zone.

Function w(x, y) (Fig 9) is given by equation:

w(x, y) = 0.5(1 - exp(z/10))(cos(3a)+1), if |a| < p/3
w(x, y) = 0, if |a| > p/3

where is the distance between PPAs and a = atan(y/x). (Fig. 8).

Fig. 9. The function w(x, y) that shows how much the priority index is decreased depending on distances x and y (see Fig. 8).

Component F4 can be explained as follows. Each PPA casts a cone of influence on other PPAs located closer to the infested area. The priority of all PPAs located in the cone of influence is decreased. If a PPA is located in the intersection of several cones of influence, then its priority index is reduced by the sum of effects of all these cones of influence.

The delimiting index, D, is a function of trap density, K, per sq.km. In large colonies (A >= 9 sq.km.), trap density is estimated simply as K = T/A. In small colonies (A < 9), there are only a few traps within a colony. Thus, it is better to estimate trap density including those traps that are located in the close neighborhood (within 3 km). Neighboring traps that are not located in the PPA are considered with weight = 0.1. The equation for trap density in small colonies is

K = [T + 0.1(Tn-T)]/[A + 0.1(An-A)]

The delimiting index, D, is equal to trap density, K multiplied by the adjustment coefficient, Z(A), which is a function of colony area, A:

D = K×Z(A)
Z(A) = 4 - 3*exp[-(A-1)²/900]

In small PPAs, the multiplier Z(A) is close to 1. Thus, the delimiting index is approximately equal to trap density. But in large colonies, this multiplier increases to 4. This means that the delimiting index is equal to a quadruple trap density in large PPAs. The reason behind this equation is that high trap density is not needed in large colonies. A 1 km grid can be used in large colonies rather than a 0.5 km trap grid; this 4-fold decrease in trap density is compensated by the multiplier.

Actions in a PPA are recommended according to Fig 5 based on estimated indices P and D. Delimiting threshold TD = 1.2 was determined based on the frequency distribution of index D in PPAs that were actually delimited or treated in Virginia, West Virginia, and North Carolina in 1996-2000 (Fig. 10). Most treated PPAs had the delimiting index > 1.2.

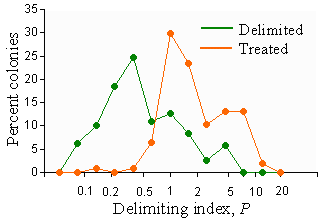
Fig. 10. Frequency distribution of the delimiting index, D, in PPAs that were delimited or treated in Virginia, West Virginia, and North Carolina in 1996-2000.

Although a few areas with D < 1.2 were treated, we generally don't recommend treatment without proper delimiting.

In most areas treated, the priority index P > 2.8 (Fig. 11). Thus, we do not recommend treatment unless P > 2.8. However, it may happen that in some years there are too many PPAs that satisfy this criterion, but resources are not sufficient to treat all these colonies. The total number of treatment blocks in 2000 is 127. It is unlikely that the number of treatments can be increased substantially in the future. Thus, we set the target target number of treatments = 130 and adjust the second priority threshold, TP₂, so that only 130 PPAs are selected for treatment. However, this threshold may appear less than 2.8, which means that some low-priority PPAs will be recommended for treatment. Thus, we do not allow reduction of the second priority threshold TP₂ below 2.8.

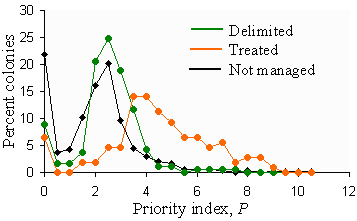
Fig. 11. Frequency distribution of the priority index, P, in PPAs that were delimited, treated, or not managed.

Historically, the number of areas delimited is approximately twice the number of areas treated. Thus, the target number of areas to delimit is 260. But the first priority threshold is not reduced below the value TP₁ = 2.3 and is not increased above the second priority threshold (Fig. 5). Actual values of the first and second priority thresholds are listed below tables of colony characteristics.

The results of the decision algorithm can be overruled in the following exceptional cases:

If maximum moth counts in a PPA > 20 then the area is managed even if the priority index is below the threshold of 2.8. Delimiting or treatment is recommended depending on the index of delimiting.
If the PPA was delimited in the previous year and maximum moth counts = 3 then no action is recommended for the next year.
If the PPA was delimited in the previous year and maximum moth counts = 4 then treatment is not recommended for the next year. Treatment recommendation is replaced by delimiting.

Typical decision making goes in the following sequence (Fig. 12). Initially, the base 2 km grid of traps is set in the area. The data on moth counts are used for planning activities in the next year. If the priority index of the PPA exceeds the threshold of 2.8, then the area is recommended for delimiting in the following year with a 0.5-km (or 1 km if the PPA > 130 sq.km.) grid of traps. In the next year, if the P ³ 2.8 and D ³ 1.2 (the latter condition is always met if delimiting was planned correctly), then the area is recommended for treatment with pesticides, Bt, virus, or mating disruption in the following year. If the priority index is below the threshold of 2.8, then the area is returned to a base 2 km grid. In the year of treatment with pesticides, Bt, or virus, a post-treatment 0.5-km grid of traps is set to evaluate the success of treatment. In this scheme (Fig. 12), post-treatment grids are not distinguished from delimiting grids. If mating disruption is used, then the base grid of traps (2 km trap spacing) is set in the year of treatment, and a post-treatment evaluation grid is set in the following year.

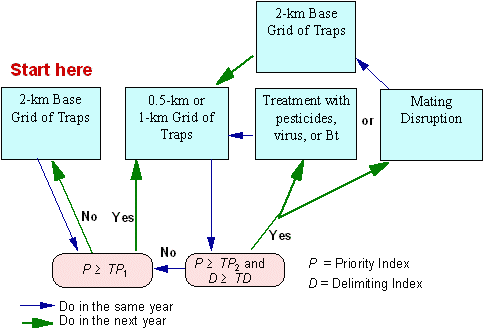
Fig. 12. Typical flowchart of the decision making in the STS project.

The decision algorithm is based on moth counts in pheromone traps. Although any search for life-stages is not cost-effective, some life-stages can be found accidentally during other kinds of activity (e.g., setting traps). In this case, we suggest setting a delimiting grid around the location where life stages were found and/or use ground treatment in accordance with quarantine rules.

The algorithm recommends areas for treatment only if they were delimited in the previous year. Treatment without delimitation is ineffective and may be expensive because it is not well-targeted.

Intensive dispersal of male moths may hamper detection and delineation of isolated colonies in some regions. Then male moth counts are relatively uniform over large areas and the decision algorithm does not suggest any areas for treatment. In this case, treatment decisions should be postponed until the year when moth dispersal will be less intensive and isolated colonies will be clearly delineated.

Post-treatment grids of traps are used for determining the success of individual treatments. They are set in the year of treatment, except after mating disruption. The effect of mating disruption can not be evaluated in the year of treatment because traps will not catch moths in a pheromone-saturated environment. Thus, a post-treatment grid of traps is set in the following year. But in the year of treatment, a 2-km grid is used simply to make sure that the concentration of pheromone was sufficient to interrupt moth movement to traps.

References Cited

Sharov, A. A., and A. M. Liebhold. 1997. Quantitative Analysis of Gypsy Moth Spread in the Central Appalachians. In J. Braumgartner, P. Brandmayer and B.F.J. Manly, eds. Population and Community Ecology for Insect Management and Conservation. Balkema, Rotterdam (in press).
Sharov, A. A., E. A. Roberts, A. M. Liebhold and F. W. Ravlin. 1995. Gypsy moth (Lepidoptera: Lymantriidae) spread in the Central Appalachians: three methods for species boundary estimation. Environ. Entomol. 24: 1529--1538.
Sharov, A. A., A. M. Liebhold, and E. A. Roberts. 1996. Spread of gypsy moth (Lepidoptera: Lymantriidae) in the Central Appalachians: comparison of population boundaries obtained from male moth capture, egg mass counts, and defoliation records. Environ. Entomol. 25: 783--792.
Sharov, A. A., A. M. Liebhold, and E. A. Roberts. 1997. Methods for Monitoring the Spread of Gypsy Moth (Lepidoptera: Lymantriidae) Populations in the Appalachian Mountains. J. Econ. Entomol. 90: 1259-1266.
Sharov, A. A., B. C. Pijanowski, A. M. Liebhold, and S. H. Gage. 1998a. What Affected the Rate of Gypsy Moth (Lepidoptera: Lymantriidae) Spread in Michigan: Winter Temperature or Forest Susceptibility? Environ. Entomol. (in review).
Sharov, A. A., A. M. Liebhold, and E. A. Roberts. 1998b. Optimizing the Use of Barrier Zones to Slow the Spread of Gypsy Moth (Lepidoptera: Lymantriidae) in North America. J. Econ. Entomol. 91: 165-174.

FAQ

1. Why did the decision algorithm select the area around the trap that caught 5 males and did not select the trap that caught 8 males?

This may happen in the following cases:
A. The trap that caught 8 males was surrounded by numerous traps that caught nothing, whereas the trap with 5 males was surrounded by traps with positive catches. Thus, interpolated moth counts may appear higher for the trap that caught 5 males than for the trap that caught 8 male moths.
B. The trap that caught 8 males was in a dense grid of traps with generally very low moth counts, whereas the trap with 5 males was in a sparse grid of traps (e.g., 5-km grid) or at the edge of the project area. Because the latter trap was relatively isolated, it was not averaged with other traps and the interpolated value appeared high.
C. The trap with 8 males may be located much closer to the population front than the trap with 5 moths. The priority of PPAs decreases with increasing distance from the population front.

2. The decision algorithm selected a very small area for a delimiting grid. Do we need to set such a small grid?

Not necessarily. The decision algorithm does not make a decision, it only suggests which areas may be considered for setting delimiting grids of traps. If the area selected by the algorithm is too small, it may be necessary to include neighboring areas into the delimiting grid.

3. Only a portion of the area with high moth counts was selected by the decision algorithm for treatment. Should we leave the remaining portions untreated?

Usually, this happens if the isolated infestation is large. This situation is common when the STS strategy is applied for the first time and colonies were not treated before. Large infestations are difficult to eradicate in one year. Depending on available funds, you may select a larger or a smaller area for treatment. The population will be monitored in subsequent years, and treatment can be applied later to eradicate remaining portions of the infestation.

Back to STS Decision-Support page

For more information, please contact Patrick Tobin or Andy Roberts
Maintained By Jiang Wu