1. Evaluation Criteria

Evaluation of the project is based on determining if the rate of gypsy moth spread has decreased as a result of pest management activities in the project. The rate of population spread in a specific year can be determined as a distance between population boundaries in consecutive years.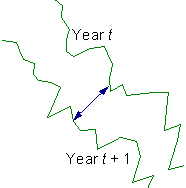

Fig. 1. The rate of spread is equal to the distance between population boundaries in consecutive years.

A population boundary is a line that separates areas where population numbers are generally above and below a specific threshold, T. Population boundaries are estimated using the Best Cell Classification Method (Sharov et al. 1995 [reprint]). We used male moth captures in pheromone traps to monitor the progression of the population front. Population boundaries were estimated for thresholds of 1, 3, 10, 30, 100, and 300 moths/trap (see the map).

The distance between two boundary lines can be determined using the two methods shown in Fig. 2. In this figure, we rotated the coordinate system so that boundary lines become approximately parallel to the X-axis.

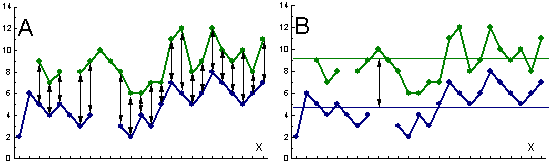Fig. 2. Two methods for estimating the distance between boundary lines: (A) averaging the distance between each pair of points, and (B) estimating the distance between averaged points in each line. Note that some local boundary points are missing.

If boundaries were estimated without missing values, then both methods would give the same result. However, with missing values (Fig. 2), results may be different. We used both methods. The rates of spread were estimated for each of 6 moth count thresholds (1, 3, 10, 30, 100, and 300 moths/trap) and then averaged.

Another evaluation criterion is the change in inter-boundary distance (distance between population boundaries for various densities). A simple model shows that inter-boundary distance should be proportional to the rate of population spread (Fig. 3).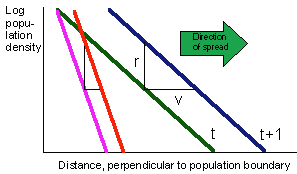

Fig. 3. Inter-boundary distance is proportional to the rate of population spread, v, if the rate of population growth, r = ln[N(t+1)/N(t)], is constant.

Long-distance dispersal of the gypsy moth occurs mostly due to inadvertent transportation of life stages by humans. After an isolated colony is established, its growth is autonomous and does not depend on subsequent immigration. Thus, we assume that the rate of population growth, r, does not depend on the age of the colony unless the population reaches its carrying capacity and defoliation starts. Thus, the inter-boundary distance should decrease if the rate of spread is being reduced by the STS project. We call this effect "boundary compression" (Fig. 4).

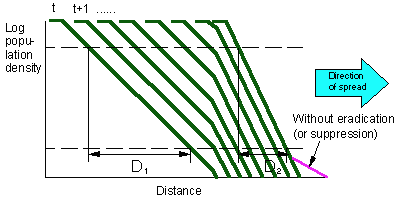Fig. 4. "Compression" of population boundaries as a result of slowing the spread of the population. D1 and D2 are inter-boundary distances before and after the start of the project.

2. Data Analysis

Thus, the only option was to compare evaluation criteria before and after the start of the STS project. However, the official start of the STS project (1993) did not coincide with the actual implementation of the pest-management strategy targeted at low-density isolated colonies. In fact, this strategy began in 1990 as a part of the Appalachian Integrated Pest Management (AIPM) program. Thus, we compared two data sets collected in the Central Appalachians before and after 1990 in the area between yellow dashed lines on this map.

Methods of data collection are described among components of the Decision-Support system. The accuracy of evaluation criteria depends on the size of evaluation zone, the number of replications in different years, and intertrap distance. Analysis of spread rate autocorrelations indicated that the size of the evaluation zone should be not less than 100 x 100 km. No autocorrelation in spread rate over time was detected, and therefore, data from different years are true replications which can increase precision for comparison of boundary changes.

Intertrap distance in the evaluation zone was 3 km in 1994, and we are examining the possibility of increasing the intertrap distance in order to reduce project costs. The error of population boundary estimates has two components: statistical error (sampling and interpolation errors) and natural variability of the boundary which are related to the variability of local factors, e.g., wind direction or forest composition.

In order to evaluate the statistical error of boundary estimates, historical AIPM trapping data were subdivided into two portions and boundaries were estimated independently using each half of the data. The standard error of average boundary position (averaged along the boundary) was 1.23 km. Natural variability of average boundaries was measured as the interaction of two factors: year x population threshold. This interaction indicated the error of 6.28 km. Rates of spread were analyzed in the same way. The results are: statistical error = 1.53 km, and natural variability error = 5.62 km.

We analyzed 5- and 10-km grids extracted from the AIPM data and found that even for a 10-km grid, statistical error (2.5 km) was less than a half of the natural variability.

Thus, natural variability of population boundaries was larger than statistical error. Hence, investment in intensive sampling in order to increase statistical precision is not justified. The intertrap distance in the evaluation zone can be increased to 5 or 8 km without any loss in precision.

3. Results

Fig. 5. Gypsy moth spread rates (average for all population thresholds).

Inter-boundary distance (estimated between neighboring boundaries in the same year) significantly declined from 1988 to 1995 which may indicate "boundary compression":

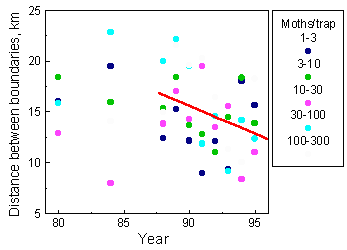Fig. 6. Inter-boundary distance in 1980-95; regression is estimated for 1988-95.

Interboundary distance in 1980-1984 was unexpectedly small (Fig. 6) as compared with large spread rates in these years (Fig. 5). In 1980, most boundaries were located outside of the mountain region where we estimated the distance between boundaries. Thus, there may be not enough data in 1984. However, in 1980 boundaries were complete and still the distance between them was small.

Conclusion: The rate of gypsy moth population expansion in the Central Appalachians has reduced after 1990 which may have resulted from suppression and eradication of gypsy moth colonies in the STS project.

References

Back to STS Decision-Support System